中国人民大学高瓴人工智能学院长聘教授孙浩团队在Nature子刊Nature Computational Science（《自然-计算科学》）发表题为“Discovering physical laws with parallel symbolic enumeration”的Article文章，提出了一种称为并行符号枚举（Parallel Symbolic Enumeration，PSE）的符号回归方法，该方法以创新的并行符号回归网络（Parallel Symbolic Regression Network，PSRN）为核心，能够从有限的观测数据中高效、准确地发现其背后隐藏的物理规律等数学表达式。文章第一作者为阮恺（博士生），通讯作者为孙浩。

这是人大高瓴人工智能学院首次在《自然-计算科学》发表论文。此前，孙浩团队已经在《自然-机器智能》《自然-通讯》上共发表4篇论文。《自然-计算科学》聚焦计算技术与数学模型的开发及应用，致力于解决跨学科科学难题。涵盖从突破性算法到创新计算方法的研究，旨在推动科研进步并解决现实挑战。

从数据中自动发现简洁、可解释的数学表达式（即符号回归），是推动现代科学研究的关键，在天文、材料、物理和生物等领域具有广泛的应用前景。然而，符号回归的核心挑战在于其巨大的搜索空间，潜在表达式的数量会随着复杂度的增加而组合爆炸，这是一个NP难问题。现有的算法，如遗传编程、深度学习等，在处理复杂问题时面临着准确性和效率的瓶颈，它们通常独立评估每一个候选表达式，导致了大量的重复计算，不仅效率低下，而且难以发现复杂、高维问题背后的真实规律，成为制约该领域发展十余年的难题。

为此，研究团队提出了并行符号枚举（PSE）新方法（图1），旨在突破符号回归的效率与准确性瓶颈。该方法的核心是一种创新的并行符号回归网络（PSRN）。与传统方法不同，PSRN能够自动识别并复用不同数学表达式中的公共子树，从根本上避免了冗余计算。同时，该网络充分利用GPU的并行计算能力，可在数秒内同时评估数亿个候选表达式，实现了搜索效率的指数级提升。通过与令牌生成器（如遗传编程）的迭代结合，PSE能够逐步构建并发现深层次的复杂公式。

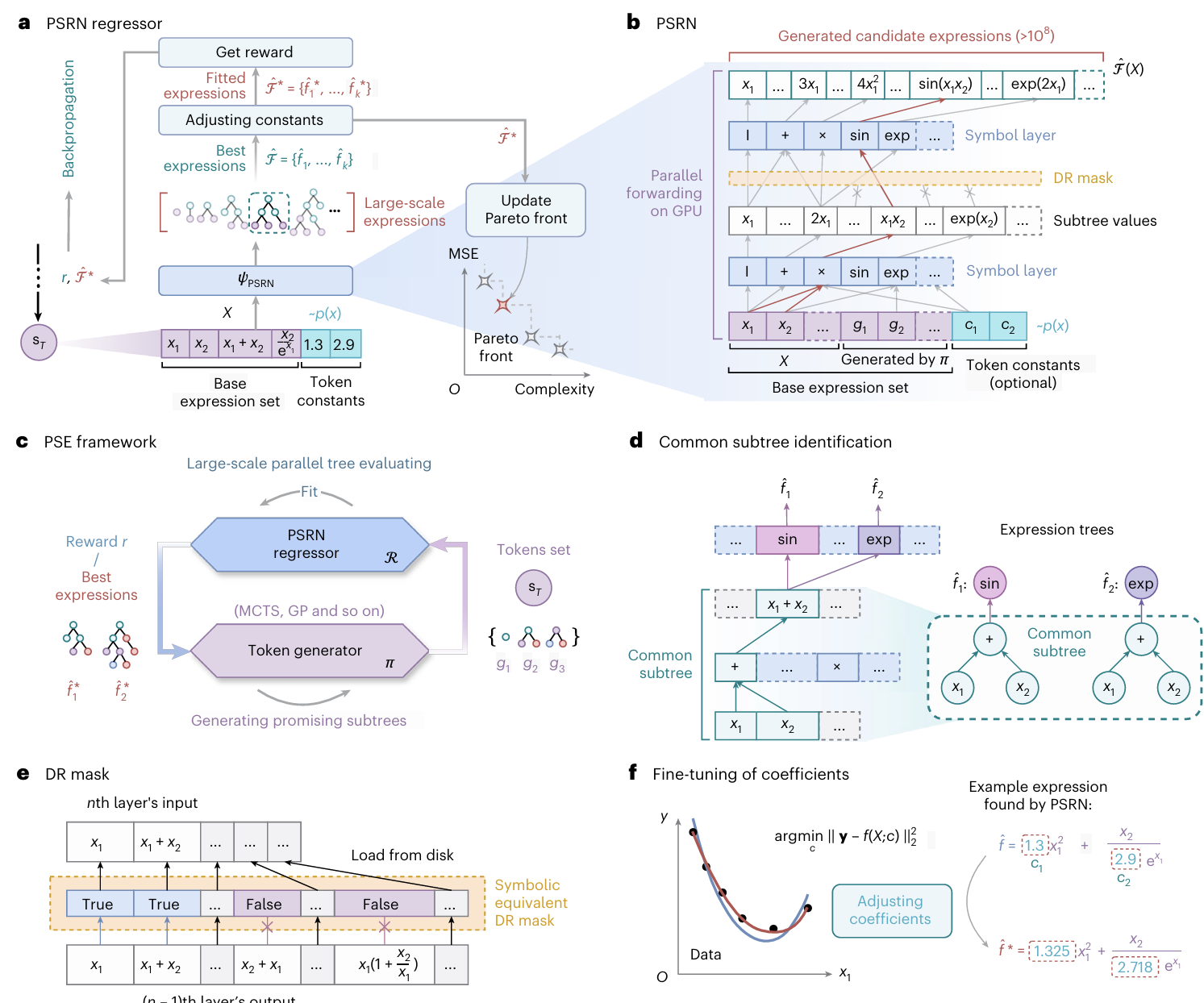
图1 | PSE模型概览。a) PSRN回归器生成候选表达式，通过误差评估得到最优表达式，再经最小二乘法微调系数后更新帕累托前沿。b) PSRN前向计算将数据张量并行处理，通过多个符号层生成海量子树值，最终输出数亿候选表达式。c) 标记生成器与PSRN回归器形成闭环，驱动表达式持续优化。d) 公共子树识别使不同表达式可复用相同子树计算结果，显著减少冗余运算。e) 去重掩码层通过屏蔽符号等价表达式，有效降低GPU显存占用。f) 对表达式系数进行微调。

研究团队在超过200个涵盖合成基准（图2）和真实物理实验（如混沌动力系统（图3）、机电定位系统、湍流摩擦定律（图4））的符号回归问题集上系统验证了PSE的性能。实验结果表明，与当前国际主流算法相比，PSE在符号恢复准确率上大幅提升，同时计算速度快一个数量级以上，展现了卓越的准确性、效率和可扩展性。

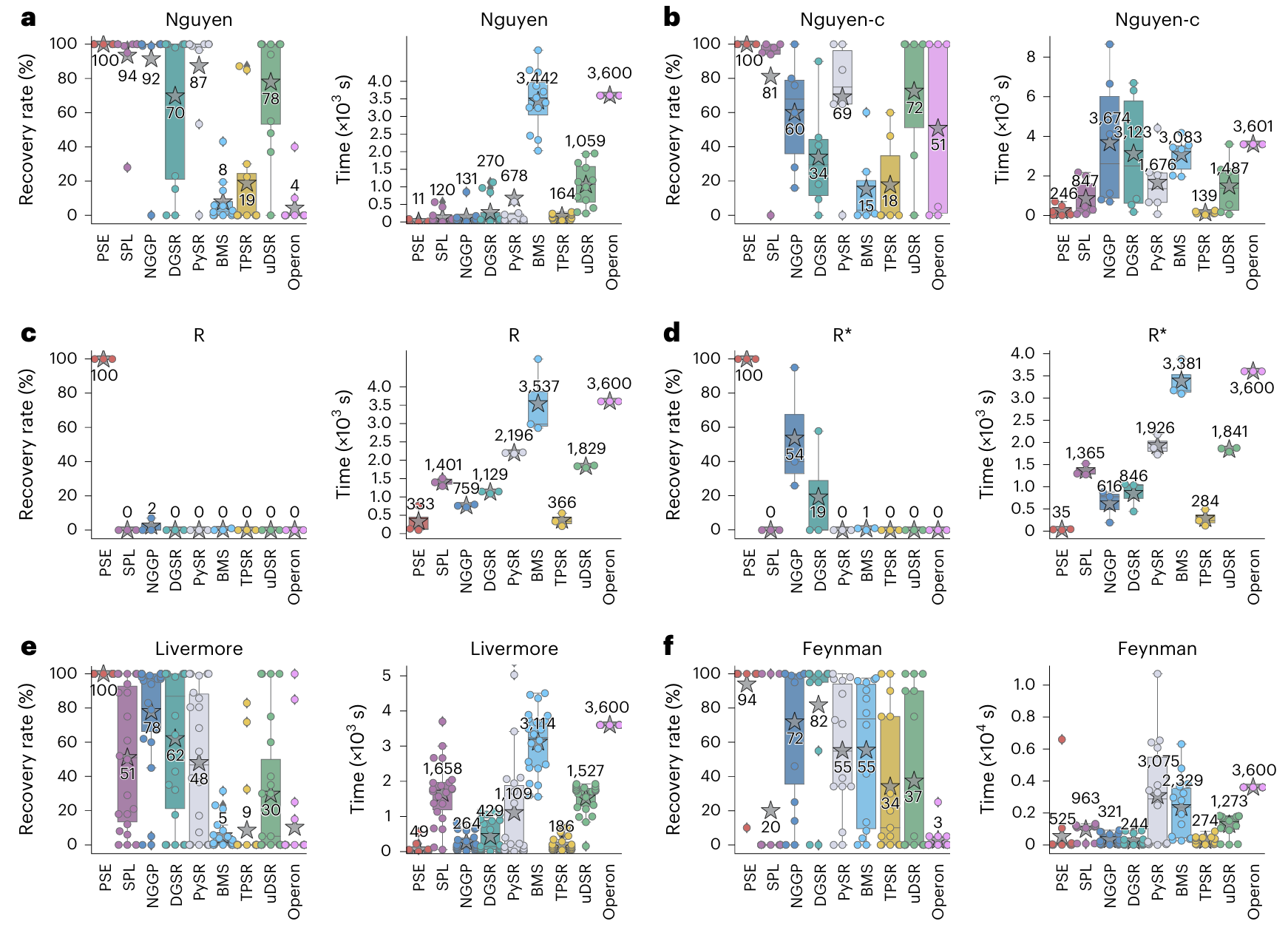
图2 | 各模型在符号回归基准测试中的性能对比。采用符号恢复率（左）和运行时间（右）两项指标评估，PSE方法在所有基准集上均取得最高恢复率且耗时最短。

自然界中普遍存在的非线性动力学系统通常由一组微分方程所支配。从有限的观测数据中提炼出这些控制方程，对于深入理解其内在机理至关重要。为此，研究团队测试了PSE模型发现多维自主混沌动力学系统控制方程的能力。

实验使用带噪声的轨迹数据，在给定一组候选算子和有限的计算时间预算下，对PSE及多种基准模型进行了实验（图3）。即使在数据存在噪声干扰的情况下，PSE模型依然能以更高的符号恢复率准确辨识出潜在的控制方程。这一结果证实了PSE在处理复杂动力学系统辨识问题时，具备出色的准确性和效率。

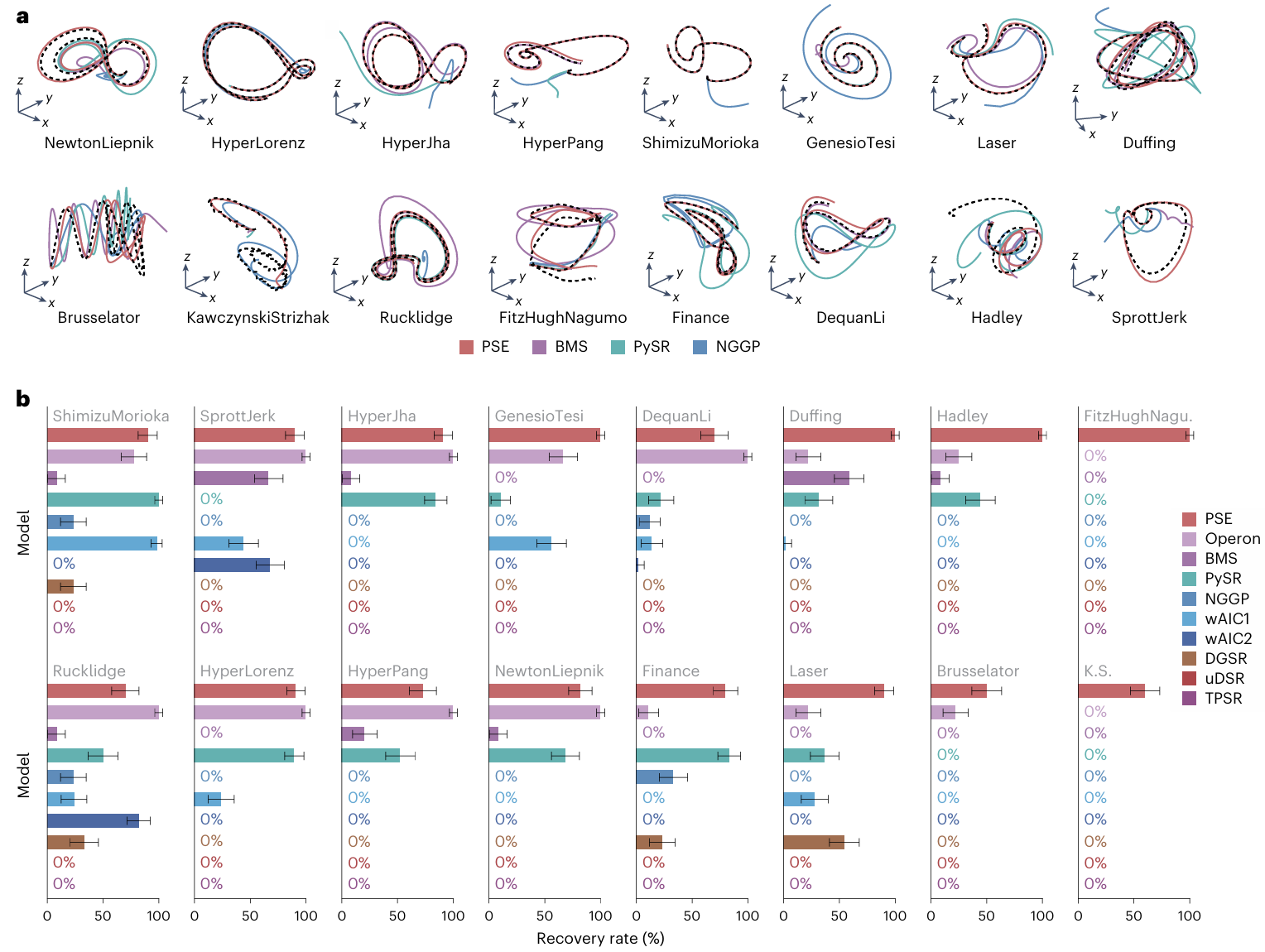
图3 | 不同模型对非线性混沌动力学方程的数据驱动发现对比。在计算时间预算相同的情况下，PSE找到真实控制方程的概率最高。各模型运行时间均限制在10分钟以内。

为了进一步验证PSE在真实物理场景中的能力，研究团队将其应用于处理充满复杂噪声与非线性的真实实验数据。测试场景包括两个经典物理问题：一是机电定位系统的动力学建模，二是探索湍流摩擦定律。

在机电定位系统实验中，寻找其控制方程对于设计更优的控制器和优化系统参数至关重要。实验评估的核心是平衡预测误差与模型复杂度，以获得一个既符合数据又简洁可解释的方程。而在流体力学领域，发现一个能够统一描述雷诺数、相对粗糙度与摩擦系数之间关系的公式，一直是该领域的一项基本挑战。（图4）在这两项基于真实实验数据的任务中，PSE均表现出色：它不仅能达到甚至超越其他方法的拟合精度，还能生成更为简洁的符号表达式，在预测精度和模型简洁性之间取得了最佳平衡。

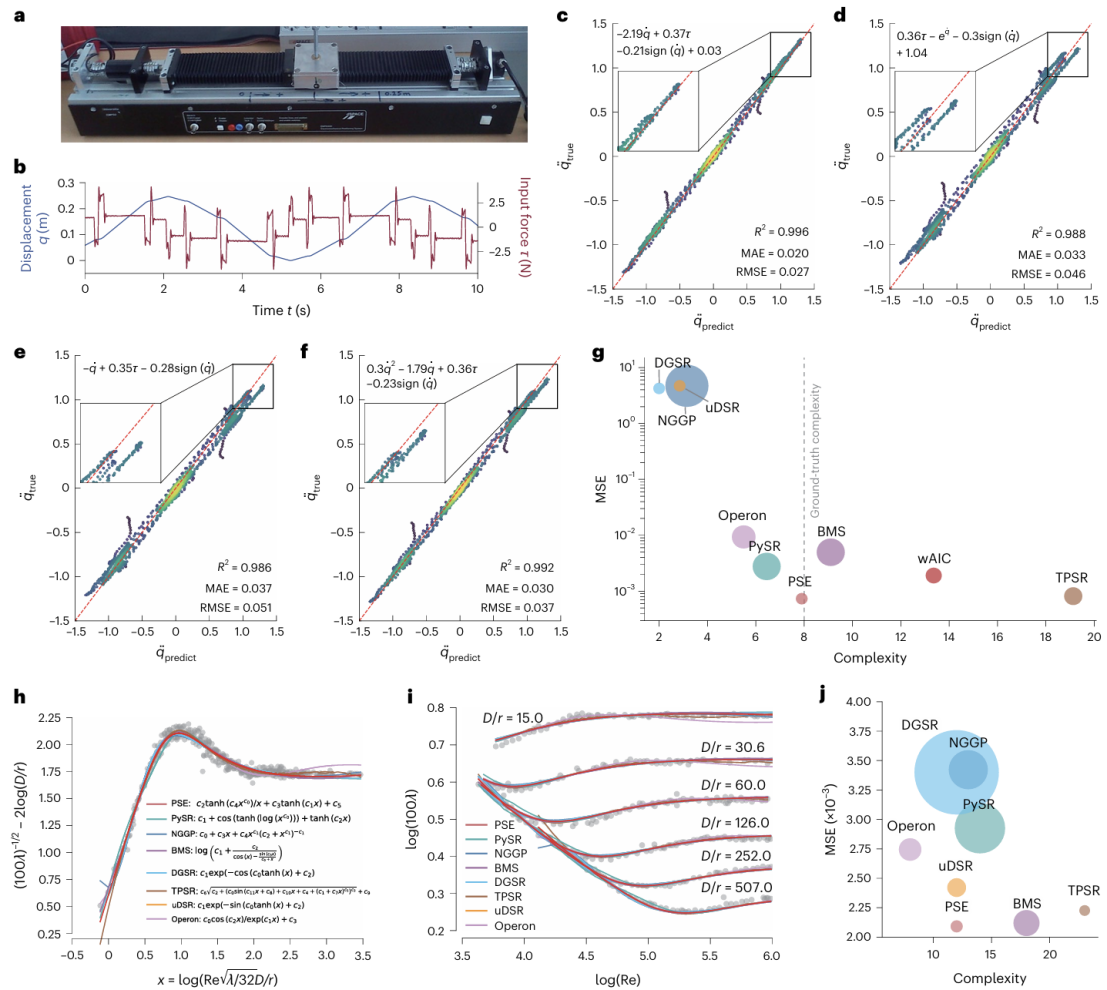
图4｜用实验数据发现物理规律。通过机电定位系统实验采集数据，对比了多种领先方法的性能。结果显示，PSE方法在预测精度和模型简洁性方面表现最优，能够找到更简洁准确的数学公式。

该工作为数据驱动的科学发现提供了一个高效、可扩展的计算框架，为自动化科学探索开辟了新路径，有望加速物理、材料、天文和生物等多个交叉学科领域的科学探索进程。该研究受国家自然科学基金、北京市自然科学基金资助。

论文链接：

https://www.nature.com/articles/s43588-025-00904-8

开源代码：

https://github.com/x66ccff/PSRN