On August 29, the VLDB 2024 International Conference on Data Management and Databases, officially announced the list of awarded papers. The paper "Optimal Matrix Sketching over Sliding Windows" co-authored by Professor Zhewei Wei's team, Professor Zengfeng Huang of Fudan University, and Dr. Feifei Li of Alibaba Group won the Best Research Paper Nominations. Professor Zhewei Wei is the corresponding author of this paper, and he and Assistant Professor Zhang Xiao's master's student Hanyan Yin, doctoral students Dongxie Wen and Jiajun Li are student authors. The VLDB (International Conference on Very Large Data Bases) conference is one of the three top international academic conferences in the field of data management and databases, and is recommended by the China Computer Federation (CCF) as a Class A international conference. The VLDB 2024 conference was held in Guangzhou from August 26 to 30, 2024.

Paper introduction: The optimization of matrix sketching algorithms over streaming data and their applications in online machine learning have received increasing attention. This paper focuses on an open problem in the field of streaming data mining and learning: "What is the minimum space overhead required to approximate an N×d matrix with an error of ε over a sliding window vector stream?" Our work proves that the space complexity of any deterministic algorithm is at least a lower bound of Ω(d/ε), and proposes a deterministic algorithm that achieves this optimal space complexity lower bound. Previously, the matrix sketching algorithm over sliding windows with the lowest asymptotic space complexity was proposed by Professor Zhewei Wei's team, Dr. Feifei Li from Alibaba Group, et al. in the paper “Matrix Sketching Over Sliding Windows” published at SIGMOD 2016: Approximate an N×d matrix with an error of ε requires O(d/ε⋅log(1/ε)) space. Since this work only studies how to combine the Frequent Directions algorithm in streaming data scenarios with the general sliding window algorithm framework, and these frameworks usually require additional space overhead, the space complexity of this algorithm differs from the optimal bound Ω(d/ε) by a coefficient term log(1/ε).

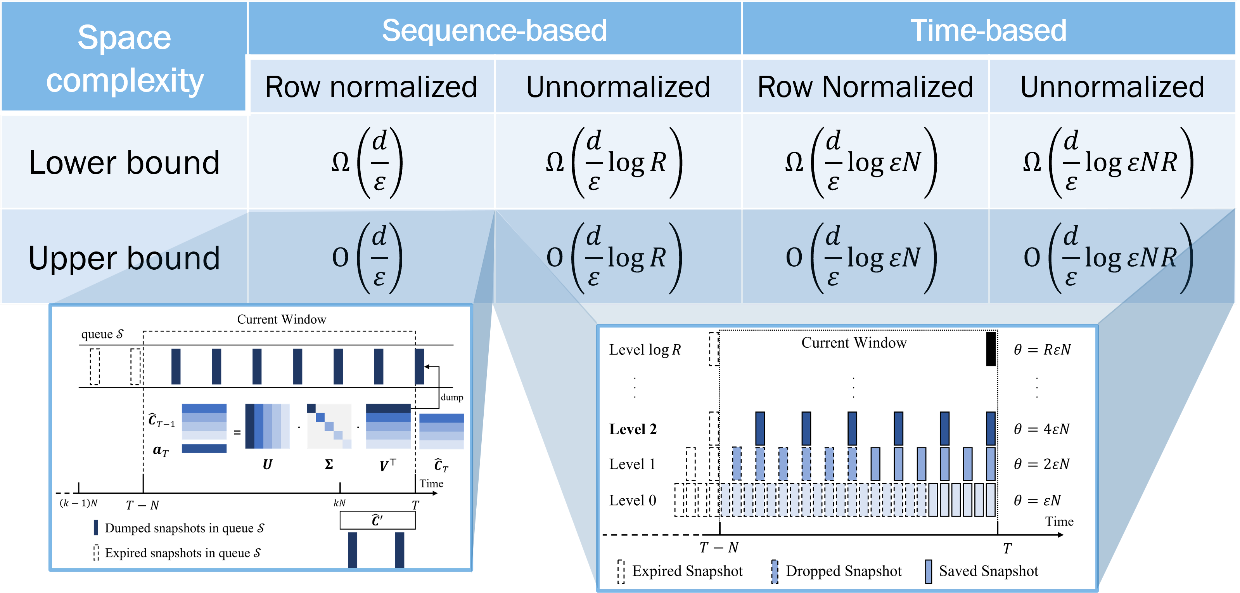
After eight years of exploring the Frequent Directions algorithm in the sliding window scenario, the original research team finally completed the study on the optimal bound and designed a simple algorithm that achieves it. Extensive experiments on synthetic and real-world data streams demonstrated that the algorithm's space efficiency surpasses that of the baseline, confirming its theoretical and experimental effectiveness. This work offers a more efficient implementation of a matrix sketching algorithm for optimizing online learning algorithms.